NCKH Giáo viên
Quasi-steady flow dynamics study of human aortic valve: an evaluation with numerical techniques
C.H Hsu(1), H.H Vu(1), B.S Nguyen(1), Y.H Kang(2)
1. Department of Mold and Die Engineering and Graduate Institute of Applied Sciences National Kaohsiung University of Applied Sciences, Kaohsiung City, Taiwan
2. Department of Mechanical Engineering and Graduate Institute of Applied Sciences National Kaohsiung University of Applied Sciences, Kaohsiung City, Taiwan
ABSTRACT
Human aortic valve, one of the four valves in the heart, is made of thin collagen type tissue. The three valve leaflets open and close under fluid forces exerted upon them to prevent blood once it is in the aorta from returning to the heart. The dysfunctions of the aortic valve compromises cardiovascular regulation and may severely affect quality of life. To solve these diseases, we need to consider the effect of the blood flow on the wall and the valve leaflets. To simulate the hemodynamics characteristics of the blood flow, ANSYS CFX10.0 software was utilized to analyze the three-dimensional Reynolds-averaged Navier-Stokes equation. With a quasi-steady analysis model, the author predicts values of the blood velocity and the wall shear stress both over the valve leaflets and the endothelial lining. Analysis results highlight that the shear stress distribution and vortex flow regime are serious affected by the leaflet opening situation and valve geometry. Maximum shear stress takes place near the center of leaflet trailing edge and near the aortic root where jet impingement takes place. The analysis results can be used to specify the requirements of crucial criteria of prosthesis aortic valve and to optimize the prosthesis aortic design.
Keywords:aortic valve, hemodynamic characteristics, wall shear stress
The viscous drag (shear stress) provided by flowing blood exerts a potent atheroprotective effect [1]. This is evidenced by the finding that atherosclerotic lesions preferentially develop in areas with turbulent flow, whereas regions with uniform laminar flow are protected ([2]). The endothelial lining is the primary sensor of wall shear stresses, and functions as a transducer of these biomechanical stimuli into biological responses within the vessel wall ([2],[3],[4]). The shear stress is highly dependent upon the direction of blood issuing through the orifice of human aortic valve and the location of blood jet impingement. Problems of thrombosis, hemolysis and endothelial lining damage are highly related to hemodynamic analysis of the aortic valves flow regime. Although a number of in vitro techniques are used for studying aortic valve flow and extracting information from the flow ([5], [6]), each has its own special difficulties as well as advantages and each can give only certain data. It is therefore necessary to use several techniques in a complementary manner to gain more aspects of hemodynamic through heart valves. On the other hand, the numerical simulation of flow through heart valves provides an entirely noninvasive method for obtaining quantitative data for velocity and shear stress distributions in the regime. Computational fluid dynamics (CFD) have become popular to determine areas of high fluid stress in the vicinity of heart valves and to improve upon existing artificial valve designs [7]. It is noted that CFD techniques can provide full domain information about flow properties including those yielded by in vitro setup and those cannot. CFD has become a more powerful tool not only for heart valve analysis but also for prosthetic heart valve design with recent improvements in computer hardware and software.
There exists a requirement to setup a threedimensional numerical model for the analysis to comprehend the complex flow pattern through human aortic valves, for example prior to development and fabrication of a prosthetic valve. This is mainly because that a prosthetic aortic valve with poor geometry design can form a substantial flow obstruction at the ventricle. Since aortic valve geometry affects the flow velocity, it also affects the shear stresses across the leaflets and aortic root. The present work utilizes a quasi-steady three dimensional CFD model to understand the complex flow pattern through human aortic valves and concentrates on the analysis of the wall shear stress over the leaflets and endothelial lining.
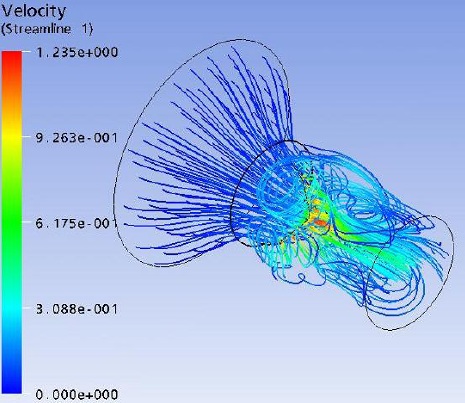
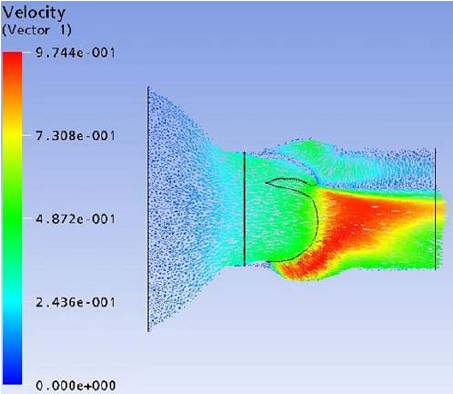
Flow field streak lines and Velocity distribution at x-z plane
REFERENCES
1. Gimbrone, M.A., Nagel, T., and Topper, J.N. (1997), “Biomechanical activation: an emerging paradigm in endothelial adhesion biology,” J. Clin. Invest., Vol. 99, pp.1809–1813.
2. Gimbrone, M.A., Topper, J.N., Nagel, T., Anderson, K.R., and Garcia-Cardena, G. (2000), “Endothelial dysfunction, hemodynamic forces, and atherogenesis,” Ann. NY Acad. Sci., Vol. 902, pp.230–240.
3. Traub, O., and Berk, B.C. (1998), “Laminar shear stress: mechanisms by which endothelial cells transduce an atheroprotective force,” Arterioscler. Thromb. Vasc. Biol., Vol. 18, pp.677–685.
4. Chien, S., Li, S., and Shyy, Y.J. (1998), “Effects of mechanical forces on signal transduction and gene expression in endothelial cells,” Hypertension, Vol. 31, pp.162–169.
5. Akutsu, T. and Saito, J. (2006), “Dynamic particle image velocimetry flow analysis of the flow field immediately downstream of bileaflet mechanical mitral prostheses,” Journal of Artificial Organs, Vol. 9, pp.165-178.
6. Lee, H., Tatsumi, E., Homma, A., Tsukiya, T. and Taenaka, Y. (2006), “Mechanism for cavitation of monoleaflet and bileaflet valves in an artificial heart,” Journal of Artificial Organs, Vol. 9, pp.154-160.
7. Ge, L., Jones, S.C., Sotiropoulos, F., Healy, T.M. and Yoganathan, A.P. (2003), “Numerical simulation of flow in mechanical heart valves: grid resolution and the assumption of flow symmetry,” ASME Transaction: Journal of Biomechanical Engineering, Vol. 125, pp.709-718.
8. Swanson, W.M. and Clark, R.E. (1973), “Aortic Valve Leaflet Motion During Systole,” Circulation Research, Vol. 32, pp.42-48.
9. Hsu, C.H. (1995), “A visualization design environment for quick designs of prosthetic mechanical heart valves,” Ph.D. Thesis, Dept. of Mechanical Engineering, Leeds University, U.K.
10. Swanson, W.M. and Clark, R.E. (1974), “Dimensions and Geometric Relationships of the Human Aortic Value as a Function of Pressure,” Circulation Research, Vol. 35, pp.871-882. The 21st International Symposium on Transport Phenomena 2010, Kaohsiung City, Taiwan
11. Walker, P.G. and Yoganathan, A.P. (1992), “In vitro pulsatile flow hemodynamics of five mechanical aortic heart valve prostheses,” Eur. J. Cardio-thorac. Surg., Vol. 6, pp.s113-123.
12. Launder, B.E. and Spalding, D.B. (1974), “The numerical computation of turbulent flows,” Computer Methods in Applied Mechanics and Engineering, Vol. 3(2), pp.269-289.
13. Patankar, S.V. (1980), Numerical Heat Transfer, Hemisphere, Washington, D.C..
14. Prakash, C. and Patankar, S.V. (1985), “A control volume based finite element method for solving the Navier-Stokes equations using equal order velocitypressure interpolation,” Numerical Heat Transfer, Vol. 8, pp.259-280.
15. King, M., David, T. and Fisher, J. (1994), “An initial parametric study on fluid flow through bileaflet mechanical heart valves, using computational fluid dynamics,” Journal of Engineering in Medicine, Vol. 208, pp.63-72.
16. Yoganathan, A.P., Woo, Y.R. and Hsing, W.S. (1986), “Turbulent shear stress measurements in the vicinity of aortic valve prostheses,” J. Biomechanics, Vol. 19, pp.433-442.
17. Fry, D.L. (1968), “Acute Vascular Endothelial Changes Associated with Increased Blood Velocity Gradients”, Circ. Res., Vol. 12, pp. 165-197.

